DevOps
Kubernetes Tutorial for Beginners: Basics, Features, Architecture
Before we start this Kubernetes tutorial, let's learn: Why you need containers? Today's internet user...
Greedy algorithms are like dynamic programming algorithms that are often used to solve optimal problems (find best solutions of the problem according to a particular criterion).
Greedy algorithms implement optimal local selections in the hope that those selections will lead to an optimal global solution for the problem to be solved. Greedy algorithms are often not too hard to set up, fast (time complexity is often a linear function or very much a second-order function). Besides, these programs are not hard to debug and use less memory. But the results are not always an optimal solution.
Greedy strategies are often used to solve the combinatorial optimization problem by building an option A. Option A is constructed by selecting each component Ai of A until complete (enough n components). For each Ai, you choose Ai optimally. In this way, it is possible that at the last step you have nothing to select but to accept the last remaining value.
There are two critical components of greedy decisions:
A greedy algorithm has five components:
In this tutorial, you will learn
With the first idea, you have the following steps of Greedy One:
However, this greedy algorithm does not always give the optimal solution. Here you have a counter-example:
With the second idea, you have the following steps of Greedy Two:
However, this greedy algorithm does not always give the optimal solution. Here you have a counter-example:
With the third idea, you have the following steps of Greedy Three. In fact, this is the most widely used algorithm.
Idea: The greedy idea of that problem is to calculate the 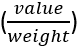 ratio of each
ratio of each  . Then sort these ratios with descending order. You will choose the highest
. Then sort these ratios with descending order. You will choose the highest  package and the capacity of the knapsack can contain that package (remain > wi). Every time a package is put into the knapsack, it will also reduce the capacity of the knapsack.
package and the capacity of the knapsack can contain that package (remain > wi). Every time a package is put into the knapsack, it will also reduce the capacity of the knapsack.
Way to select the packages:
You see this is a problem of finding max. The list of packages is sorted in descending order of unit costs to consider branching.
Pseudo code for the algorithm:
Fractional Knapsack (Array W, Array V, int M) 1. for i <- 1 to size (V) 2. calculate cost[i] <- V[i] / W[i] 3. Sort-Descending (cost) 4. i ← 1 5. while (i <= size(V)) 6. if W[i] <= M 7. M ← M – W[i] 8. total ← total + V[i]; 9. if W[i] > M 10. i ← i+1
The complexity of the algorithm:
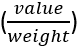 ratio of each package.
ratio of each package.
public class KnapsackPackage {
private double weight;
private double value;
private Double cost;
public KnapsackPackage(double weight, double value) {
super();
this.weight = weight;
this.value = value;
this.cost = new Double(value / weight);
}
public double getWeight() {
return weight;
}
public double getValue() {
return value;
}
public Double getCost() {
return cost;
}
}
public void knapsackGreProc(int W[], int V[], int M, int n) {
KnapsackPackage[] packs = new KnapsackPackage[n];
for (int i = 0; i < n; i ++) {
packs[i] = new KnapsackPackage(W[i], V[i]);
}
Arrays.sort(packs, new Comparator<KnapsackPackage>() {
@Override
public int compare(KnapsackPackage kPackA, KnapsackPackage kPackB) {
return kPackB.getCost().compareTo(kPackA.getCost());
}
});
int remain = M;
double result = 0d;
int i = 0;
boolean stopProc = false;
while (!stopProc) {
if (packs[i].getWeight() <= remain) {
remain -= packs[i].getWeight();
result += packs[i].getValue();
System.out.println("Pack " + i + " - Weight " + packs[i].getWeight() + " - Value " + packs[i].getValue());
}
if (packs[i].getWeight() > remain) {
i ++;
}
if (i == n) {
stopProc = true;
}
}
System.out.println("Max Value:\t" + result);
}
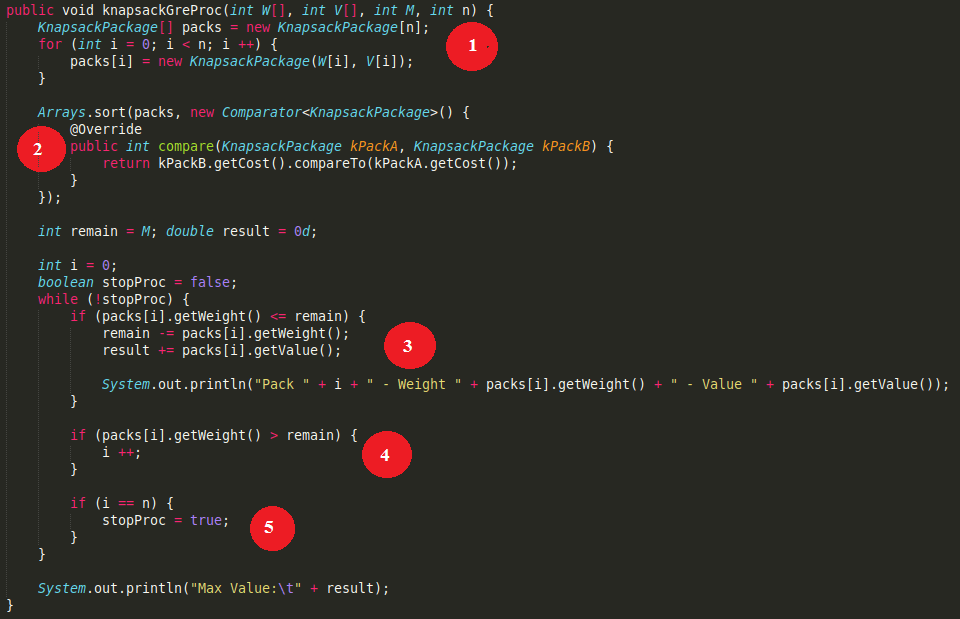
Explanation of code:
In this tutorial, you have two examples. Here is java code to run the above program with two examples:
public void run() {
/*
* Pack and Weight - Value
*/
//int W[] = new int[]{15, 10, 2, 4};
int W[] = new int[]{12, 2, 1, 1, 4};
//int V[] = new int[]{30, 25, 2, 6};
int V[] = new int[]{4, 2, 1, 2, 10};
/*
* Max Weight
*/
//int M = 37;
int M = 15;
int n = V.length;
/*
* Run the algorithm
*/
knapsackGreProc(W, V, M, n);
}
You have the output:
Pack 0 - Weight 10.0 - Value 25.0 Pack 0 - Weight 10.0 - Value 25.0 Pack 0 - Weight 10.0 - Value 25.0 Pack 2 - Weight 4.0 - Value 6.0 Pack 3 - Weight 2.0 - Value 2.0 Max Value: 83.0
Pack 0 - Weight 4.0 - Value 10.0 Pack 0 - Weight 4.0 - Value 10.0 Pack 0 - Weight 4.0 - Value 10.0 Pack 1 - Weight 1.0 - Value 2.0 Pack 1 - Weight 1.0 - Value 2.0 Pack 1 - Weight 1.0 - Value 2.0 Max Value: 36.0
Analyze the first example:
Steps for applying algorithm for the first example:
With the same analysis of the second example, you have the result: select package 4 (3 times) and package 5 (3 times).
class KnapsackPackage(object):
""" Knapsack Package Data Class """
def __init__(self, weight, value):
self.weight = weight
self.value = value
self.cost = value / weight
def __lt__(self, other):
return self.cost < other.cost
class FractionalKnapsack(object):
def __init__(self):
def knapsackGreProc(self, W, V, M, n):
packs = []
for i in range(n):
packs.append(KnapsackPackage(W[i], V[i]))
packs.sort(reverse = True)
remain = M
result = 0
i = 0
stopProc = False
while (stopProc != True):
if (packs[i].weight <= remain):
remain -= packs[i].weight;
result += packs[i].value;
print("Pack ", i, " - Weight ", packs[i].weight, " - Value ", packs[i].value)
if (packs[i].weight > remain):
i += 1
if (i == n):
stopProc = True
print("Max Value:\t", result)
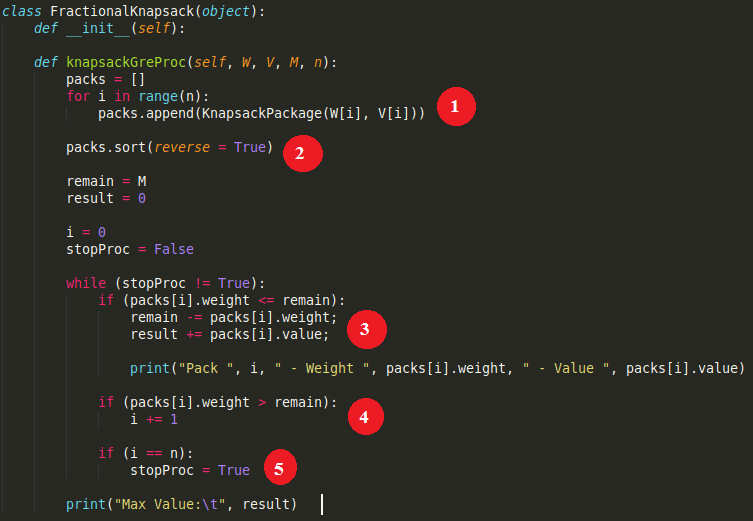
Explanation of code:
Here is Python3 code to run the above program with the first example:
if __name__ == "__main__":
W = [15, 10, 2, 4]
V = [30, 25, 2, 6]
M = 37
n = 4
proc = FractionalKnapsack()
proc.knapsackGreProc(W, V, M, n)
You have the output:
Pack 0 - Weight 10 - Value 25 Pack 0 - Weight 10 - Value 25 Pack 0 - Weight 10 - Value 25 Pack 2 - Weight 4 - Value 6 Pack 3 - Weight 2 - Value 2 Max Value: 83
using System;
namespace KnapsackProblem
{
public class KnapsackPackage
{
private double weight;
private double value;
private double cost;
public KnapsackPackage(double weight, double value)
{
this.weight = weight;
this.value = value;
this.cost = (double) value / weight;
}
public double Weight
{
get { return weight; }
}
public double Value
{
get { return value; }
}
public double Cost
{
get { return cost; }
}
}
}
using System;
namespace KnapsackProblem
{
public class FractionalKnapsack
{
public FractionalKnapsack()
{
}
public void KnapsackGreProc(int[] W, int[] V, int M, int n)
{
KnapsackPackage[] packs = new KnapsackPackage[n];
for (int k = 0; k < n; k++)
packs[k] = new KnapsackPackage(W[k], V[k]);
Array.Sort<KnapsackPackage>(packs, new Comparison<KnapsackPackage>(
(kPackA, kPackB) => kPackB.Cost.CompareTo(kPackA.Cost)));
double remain = M;
double result = 0d;
int i = 0;
bool stopProc = false;
while (!stopProc)
{
if (packs[i].Weight <= remain)
{
remain -= packs[i].Weight;
result += packs[i].Value;
Console.WriteLine("Pack " + i + " - Weight " + packs[i].Weight + " - Value " + packs[i].Value);
}
if (packs[i].Weight > remain)
{
i++;
}
if (i == n)
{
stopProc = true;
}
}
Console.WriteLine("Max Value:\t" + result);
}
}
}
Explanation of code:
Here is C# code to run the above program with the first example:
public void run()
{
/*
* Pack and Weight - Value
*/
int[] W = new int[]{15, 10, 2, 4};
//int[] W = new int[] { 12, 2, 1, 1, 4 };
int[] V = new int[]{30, 25, 2, 6};
//int[] V = new int[] { 4, 2, 1, 2, 10 };
/*
* Max Weight
*/
int M = 37;
//int M = 15;
int n = V.Length;
/*
* Run the algorithm
*/
KnapsackGreProc(W, V, M, n);
}
You have the output:
Pack 0 - Weight 10 - Value 25 Pack 0 - Weight 10 - Value 25 Pack 0 - Weight 10 - Value 25 Pack 2 - Weight 4 - Value 6 Pack 3 - Weight 2 - Value 2 Max Value: 83
The algorithm of Greedy Three resolves quickly and can also be optimal in some cases. However, in some special cases, it does not give the optimal solution. Here you have a counter-example:
Here is java code to run the above program with the counter-example:
public void run() {
/*
* Pack and Weight - Value
*/
int W[] = new int[]{7, 6, 4};
int V[] = new int[]{9, 6, 4};
/*
* Max Weight
*/
int M = 10;
int n = V.length;
/*
* Run the algorithm
*/
knapsackGreProc(W, V, M, n);
}
Here is the result:
Pack 0 - Weight 7.0 - Value 9.0 Max Value: 9.0
That's all to Fractional Knapsack problem.
Before we start this Kubernetes tutorial, let's learn: Why you need containers? Today's internet user...
What is R List? R List is an object in R programming which includes matrices, vectors, data...
MAC includes a huge collection of the built-in app. However, there are many useful software that...
In this tutorial, you will learn select() Filter() Pipeline arrange() The library called dplyr...
Video players are media player that can play video data from varieties of sources local disc, DVD, VCD,...
Instagram downloader tools are applications that help you to download Instagram videos and photos.